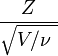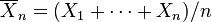- t de Student + Vdeo

En probabilidad y estadística, la distribución t (de Student) es una distribución de probabilidad que surge del problema de estimar la media de una población normalmente distribuida cuando el tamaño de la muestra es pequeño.
Aparece de manera natural al realizar la prueba t de Student para la determinación de las diferencias entre dos medias muestrales y para la construcción del intervalo de confianza para la diferencia entre las medias de dos poblaciones cuando se desconoce la desviación típica de una población y ésta debe ser estimada a partir de los datos de una muestra.

Caracterización

La distribución t de Student es la distribución de probabilidad del cociente

$\frac{Z}{\sqrt{V/\nu\ }}$

donde

Z tiene una distribución normal de media nula y varianza 1
V tiene una distribución ji-cuadrado con $\nu\$ grados de libertad
Z y V son independientes

Si μ es una constante no nula, el cociente $\frac{Z+\mu}{\sqrt{V/\nu\ }}$ es una variable aleatoria que sigue la distribución t de Student no central con parámetro de no-centralidad $\mu$ .

Aparición y especificaciones de la distribución t de Student

Supongamos que X₁,..., X_n son variables aleatorias independientes distribuidas normalmente, con media μ y varianza σ². Sea

$\overline{X}_n=(X_1+\cdots+X_n)/n$

la media muestral. Entonces

$Z=\frac{\overline{X}_n-\mu}{\sigma/\sqrt{n}}$

sigue una distribución normal de media 0 y varianza 1.
Sin embargo, dado que la desviación estándar no siempre es conocida de antemano, Gosset estudió un cociente relacionado,

$T=\frac{\overline{X}_n-\mu}{S_n/\sqrt{n}},$

donde

$S ^ 2(x) = \frac{1}{n-1} \sum_{i=1}^n (x_i - \overline{x}) ^ 2$

es la varianza muestral y demostró que la función de densidad de T es

$f(t) = \frac{\Gamma((\nu+1)/2)}{\sqrt{\nu\pi\,}\,\Gamma(\nu/2)} (1+t^2/\nu)^{-(\nu+1)/2}$

donde $\nu\$ es igual a n − 1.
La distribución de T se llama ahora la distribución-t de Student.
El parámetro $\nu\$ representa el número de grados de libertad. La distribución depende de $\nu\$ , pero no de $\mu$ o $\sigma$ , lo cual es muy importante en la práctica.

Intervalos de confianza derivados de la distribución t de Student

El procedimiento para el cálculo del intervalo de confianza basado en la t de Student consiste en estimar la desviación típica de los datos S y calcular el error estándar de la media $= \frac{S}{\sqrt{n}}$ , siendo entonces el intervalo de confianza para la media = $=\overline{X} \pm t_{\alpha/2,n-1} \frac{S}{\sqrt{n}}$ .
Es este resultado el que se utiliza en el test de Student: puesto que la diferencia de las medias de muestras de dos distribuciones normales se distribuye también normalmente, la distribución t puede usarse para examinar si esa diferencia puede razonablemente suponerse igual a cero.
para efectos prácticos el valor esperado y la varianza son:
E(t(n))= 0 y Var (t(n-1)) = n/(n-2) para n > 3

Historia

La distribución de Student fue descrita en 1908 por William Sealy Gosset. Gosset trabajaba en una fábrica de cerveza, Guinness, que prohibía a sus empleados la publicación de artículos científicos debido a una difusión previa de secretos industriales. De ahí que Gosset publicase sus resultados bajo el seudónimo de Student.

Distribución t de Student No Estandarizada

La distribución t puede generalizarse a 3 parámetros, introduciendo un parámero locacional $\mu$ y otro de escala $\sigma$ . El resultado es una distribución t de Student No Estandarizada cuya densidad está definida por:²

$p(x|\nu,\mu,\sigma) = \frac{\Gamma(\frac{\nu + 1}{2})}{\Gamma(\frac{\nu}{2})\sqrt{\pi\nu}\sigma} \left(1+\frac{1}{\nu}\left(\frac{x-\mu}{\sigma}\right)^2\right)^{-\frac{\nu+1}{2}}$

Equivalentemente, puede escribirse en términos de $\sigma^2$ (correspondiente a la varianza en vez de a la desviación estándar):

$p(x|\nu,\mu,\sigma^2) = \frac{\Gamma(\frac{\nu + 1}{2})}{\Gamma(\frac{\nu}{2})\sqrt{\pi\nu\sigma^2}} \left(1+\frac{1}{\nu}\frac{(x-\mu)^2}{\sigma^2}\right)^{-\frac{\nu+1}{2}}$

Otras propiedades de esta versión de la distribución t son:²

$\begin{align} \operatorname{E}(X) &= \mu \quad \quad \quad \text{para }\,\nu > 1 ,\\ \text{Var}(X) &= \sigma^2\frac{\nu}{\nu-2}\, \quad \text{para }\,\nu > 2 ,\\ \text{Moda}(X) &= \mu . \end{align}$