- Chi Cuadrado + Video

En estadística, la distribución χ² (de Pearson), llamada Chi cuadrado o Ji cuadrado, es una distribución de probabilidad continua con un parámetro $k$ que representa los grados de libertad de la variable aleatoria

$X = Z_1^2 + \cdots + Z_k^2$

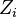donde $Z_i$ son variables aleatorias normales independientes de media cero y varianza uno. El que la variable aleatoria $X$ tenga esta distribución se representa habitualmente así: $X\sim\chi^2_k$ .
Es conveniente tener en cuenta que la letra griega χ se transcribe al latín como chi y se pronuncia en castellano como ji.

Propiedades

Función de densidad

Su función de densidad es:

$f(x;k)= \begin{cases}\displaystyle \frac{1}{2^{k/2}\Gamma(k/2)}\,x^{(k/2) - 1} e^{-x/2}&\text{para }x\ge0,\\ 0&\text{para }x<0 \end{cases}$

donde $\Gamma$ es la función gamma.

Función de distribución acumulada

Su función de distribución es

$F_k(x) = \frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

donde $\ \gamma(k,z)$ es la función gamma incompleta.
El valor esperado y la varianza de una variable aleatoria X con distribución χ² son, respectivamente, k y 2k.

Relación con otras distribuciones

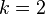La distribución χ² es un caso especial de la distribución gamma. De hecho, $X \sim \Gamma(\frac{k}{2}, \theta=2).$ Como consecuencia, cuando $k=2$ , la distribución χ² es una distribución exponencial de media $k=2$ .
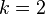Cuando k es suficientemente grande, como consecuencia del teorema central del límite, puede aproximarse por una distribución normal:

$\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{(1,\sqrt{2/k})} (x)$

Aplicaciones

La distribución χ² tiene muchas aplicaciones en inferencia estadística. La más conocida es la de la denominada prueba χ² utilizada como prueba de independencia y como prueba de bondad de ajuste y en la estimación de varianzas. Pero también está involucrada en el problema de estimar la media de una población normalmente distribuida y en el problema de estimar la pendiente de una recta de regresión lineal, a través de su papel en la distribución t de Student.
Aparece también en todos los problemas de análisis de varianza por su relación con la distribución F de Snedecor, que es la distribución del cociente de dos variables aleatorias independientes con distribución χ².