Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.
Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:
Ejemplos
Las siguientes situaciones son ejemplos de experimentos que pueden modelizarse por esta distribución:- Se lanza un dado diez veces y se cuenta el número X de treses obtenidos: entonces X ~ B(10, 1/6)
- Se lanza una moneda dos veces y se cuenta el número X de caras obtenidas: entonces X ~ B(2, 1/2)
- Una partícula se mueve unidimensionalmente con probabilidad p de moverse de aquí para allá y 1-q de moverse de allá para acá
Experimento binomial
Existen muchas situaciones en las que se presenta una experiencia binomial. Cada uno de los experimentos es independiente de los restantes (la probabilidad del resultado de un experimento no depende del resultado del resto). El resultado de cada experimento ha de admitir sólo dos categorías (a las que se denomina éxito y fracaso). Las probabilidades de ambas posibilidades han de ser constantes en todos los experimentos (se denotan como p y q o p y 1-p).Se designa por X a la variable que mide el número de éxitos que se han producido en los n experimentos.
Cuando se dan estas circunstancias, se dice que la variable X sigue una distribución de probabilidad binomial, y se denota B(n,p).
Características analíticas
Su función de probabilidad es
siendo
 las combinaciones de
las combinaciones de  en
en  (
( elementos tomados de
elementos tomados de  en
en  )
)Ejemplo
Supongamos que se lanza un dado (con 6 caras) 50 veces y queremos conocer la probabilidad de que el número 3 salga 20 veces. En este caso tenemos una X ~ B(50, 1/6) y la probabilidad sería P(X=20):Propiedades
Relaciones con otras variables aleatorias
Si tiende a infinito y
tiende a infinito y  es tal que el producto entre ambos parámetros tiende a
es tal que el producto entre ambos parámetros tiende a  , entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro
, entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro  .
.Por último, se cumple que cuando n es muy grande (usualmente se exige que
 ) la distribución binomial puede aproximarse mediante la distribución normal.
) la distribución binomial puede aproximarse mediante la distribución normal.Propiedades reproductivas
Dadas n variables binomiales independientes de parámetros ni (i = 1,..., n) y , su suma es también una variable binomial, de parámetros n1+... + nn, y
, su suma es también una variable binomial, de parámetros n1+... + nn, y  , es decir,
, es decir,
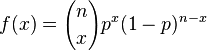

![\mathbb{E}[X] = np\,](http://upload.wikimedia.org/math/3/e/c/3ec567691d864b73ee9a0f991c0d4026.png)
![\mathbb{V}\text{ar}[X] =np(1-p)\,](http://upload.wikimedia.org/math/0/f/8/0f82ec44d890e66e62e1a266c2357104.png)
