
Por hipótesis tenemos una partición  del espacio muestral
del espacio muestral  . Por lo tanto el suceso
. Por lo tanto el suceso 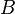 se puede escribir como
se puede escribir como
 del espacio muestral
del espacio muestral  . Por lo tanto el suceso
. Por lo tanto el suceso 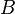 se puede escribir como
se puede escribir como
ahora bien, los conjuntos  son dos a dos disjuntos, ya que en caso contrario los
son dos a dos disjuntos, ya que en caso contrario los  tampoco lo serían. En consecuencia
tampoco lo serían. En consecuencia
 son dos a dos disjuntos, ya que en caso contrario los
son dos a dos disjuntos, ya que en caso contrario los  tampoco lo serían. En consecuencia
tampoco lo serían. En consecuencia
Por último, se sabe que  para cualesquiera sucesos
para cualesquiera sucesos  y
y  . Luego
. Luego
 para cualesquiera sucesos
para cualesquiera sucesos  y
y  . Luego
. Luego
que era lo que se quería demostrar.